Phương pháp giải các bài toán tìm min, max liên quan đến số phức
1. Kiến thức cần nhớ
- Mô đun của số phức z=a+bi là |z|=√a2+b2≥0
- Bất đẳng thức Cô-si: x+y≥2√xy với x,y>0
- Bất đẳng thức Bunhiacopxki: (a2+b2)(c2+d2)≥(ac+bd)2
- Bất đẳng thức chứa dấu giá trị tuyệt đối: ||z1|−|z2||≤|z1±z2|≤|z1|+|z2|
2. Một số dạng toán thường gặp
Dạng 1: Tìm số phức thỏa mãn điều kiện có mô đun nhỏ nhất, lớn nhất.
Phương pháp:
- Bước 1: Gọi số phức z=x+yi(x,y∈R).
- Bước 2: Thay z và biểu thức đã cho tìm mối quan hệ của x,y.
- Bước 3: Đánh giá biểu thức có được để tìm max, min, từ đó suy ra x,y⇒z.
Có thể sử dụng phương pháp hình học để giải các bài tập dạng này.
Phương pháp:
Bước 1: Tìm tập hợp điểm biểu diễn của số phức. Có 4 tập hợp điểm thường gặp
+) Đường thẳng
+) Đường tròn
+) Đường elip
+) Parabol
Bước 2: Vẽ tập hợp điểm biểu diễn của số phức. Từ đó tìm max, min của mô đun
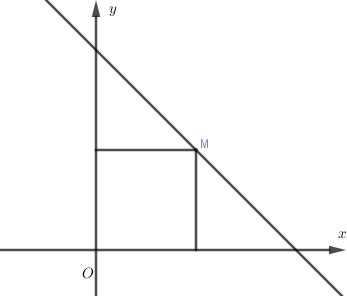
Số phức z=x+yi(x,y∈R) có điểm biểu diễn là M(x,y). Mô đun của số phức z là độ dài đoạn thẳng OM với O là gốc tọa độ.
Dạng 2: Tìm GTLN, GTNN của mô đun số phức thỏa mãn điều kiện cho trước.
Phương pháp:
- Sử dụng các bất đẳng thức Cô si, Bunhiacopxki và bất đẳng thức tam giác.
Có thể bạn quan tâm:
Tài liệu
